Statement
In spherical coordinates, a conductor at r1 is at potential V1, and a conductor at r2 is at a potential V2. The space between the conductors is a dielectric with relative permittivity e. Find the surface charge densities on the conductors.
System Parameters
Permittivity of free space:
Solution
There is no information about the shape of the conductors, and only a variation in r is indicated in the problem. The Laplace equation for the radial component in spherical coordinates (see Chapter 8) is
integrate both sides to get
Integrate a final time to get
Use the two potentials and the two distances above to find A and B. First, make a guess for A and B, and then use the equation solver to find the actual values. For more information about the equation solver (known as solve blocks in Mathcad), see A Mathcad Tutorial. Note that, since the solver uses guess to find solutions, the guesses may need to be changed if you choose to vary the starting conditions of this problem.
P.25 |
|
P.26 Laplace Equation in Spherical Coordinates |
|
|
Guess:
Where
Find the electric field from the voltage.
in the radial direction
Evaluate symbolically:
On a conductor surface, preserving the relationship between normal direction on the surface and the direction of D,
Among other things, this problem is a lesson in keeping tabs of your minus signs. There are a lot of sign flips through the problem, but you can always check your answers by thinking about the problem physically. We expect that the field lines will point from the surface of high potential to the surface of low potential, which is opposite to the unit radial vector. Therefore, E and D are negative, and the charge on the surface of lower potential is negative.
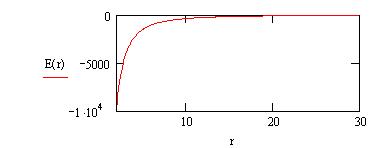
Also, examine the graph of the electric field in the radial direction. As the field approaches the surface of negative potential closer to the origin, the field strength increases to a relatively large magnitude. This is because the inner surface has a higher charge density. You can visualize this as a higher packing of negative charge on which the field lines terminate. Think about what this means in terms of the breakdown, or dielectric, strength of any material between the conductors and designing such a device. See Problem 7.4 for a review of dielectric strength.